统一压缩策略 (UCS)

统一压缩策略 (UCS) 建议用于大多数工作负载，无论是读密集型、写密集型、混合读写型还是时间序列型。无需使用传统压缩策略，因为 UCS 可以配置为表现得像任何一种策略。

UCS 是一种压缩策略，它结合了其他策略的优点以及新功能。UCS 旨在最大限度地提高压缩速度，这对于高密度节点至关重要，它使用独特的分片机制并行压缩分区数据。而 STCS、LCS 或 TWCS 在更改压缩策略时需要对数据进行完全压缩，UCS 可以动态更改参数以在一种策略与另一种策略之间切换。事实上，可以同时使用多种压缩策略的组合，并为层次结构的每个级别设置不同的参数。最后，UCS 是无状态的，因此它不依赖于任何元数据来做出压缩决策。

两个关键概念细化了分组的定义

分层压缩和分级压缩可以概括为等效的，因为两者都基于 SSTable 的**大小**（或不重叠的 SSTable 运行）创建呈指数增长的级别。因此，当一个级别上存在超过给定数量的 SSTable 时，就会触发压缩。
**大小**可以被**密度**取代，允许 SSTable 在压缩输出写入时在任意点进行拆分，同时仍然生成分级层次结构。密度定义为 SSTable 的大小除以它覆盖的令牌范围的宽度。

让我们更详细地看一下第一个概念。

读写放大

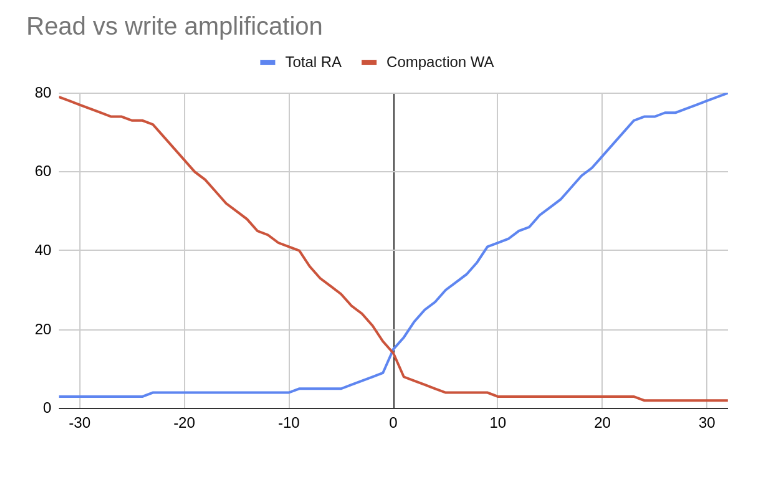
UCS 可以调整用于服务读取的 SSTable 数量（读取放大，或 RA）与数据在其生命周期内必须重写的次数（写入放大，或 WA）之间的平衡。单个可配置的缩放参数决定了压缩的行为，从读密集型模式到写密集型模式。缩放参数可以随时更改，压缩策略将相应调整。例如，操作员可能决定

降低缩放参数，以降低读取放大，但代价是在特定表读密集型且可能受益于降低延迟时进行更复杂的写入
提高缩放参数，以降低写入放大，当已确定压缩无法跟上对表的写入数量时

任何此类更改只会启动将层次结构置于与新配置兼容的状态所需的压缩。任何已完成的额外工作（例如，从负参数切换到正参数时），都是有利的，并且会被纳入。

此外，通过将缩放参数设置为模拟高分层扇出因子，UCS 可以实现与 TWCS 相同的压缩。

ucs

UCS 使用分层压缩和分级压缩的组合，以及分片，来实现所需的读写放大。SSTable 按令牌范围排序，然后分组到级别

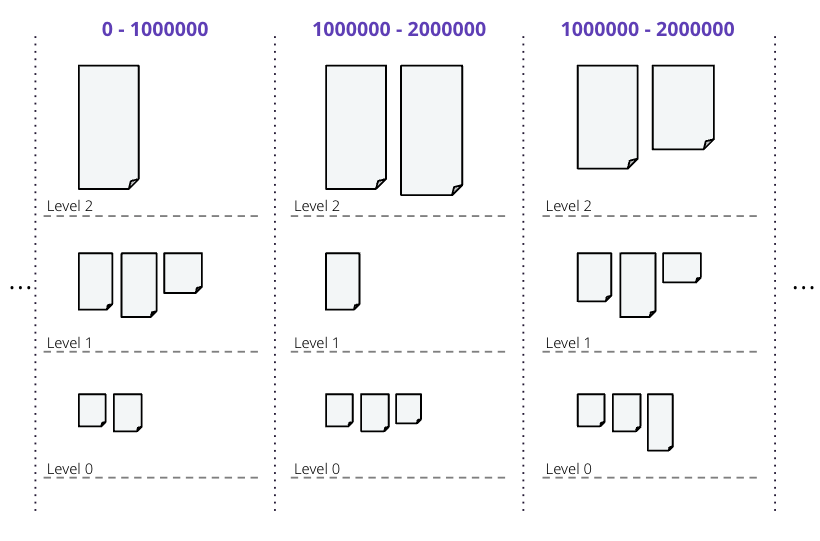
sharding

UCS 基于 SSTable 密度的对数将 SSTable 分组到级别，其中扇出因子 \(f\) 作为对数的底数，并且每个级别在拥有 \(t\) 个重叠 SSTable 时就会触发压缩。

缩放参数 \(w\) 的选择决定了扇出因子 \(f\) 的值。反过来，\(w\) 将模式定义为分级或分层，并且 \(t\) 设置为分级压缩的 \(t=2\) 或分层压缩的 \(t=f\)。最后一个参数，最小 SSTable 大小，是确定 UCS 的完整行为所需的。

根据 \(w\) 的值，可以实现三种压缩类型，如上图 RA 和 WA 所示

分级压缩，高 WA，低 RA：\(w < 0\)，\(f = 2 - w\) 且 \(t=2\) \(L_{f}\) 是指定此范围 \(w\) 值的简写（例如，\(w=-8\) 的 L10）。
分层压缩，低 WA，高 RA：\(w > 0\)，\(f = 2 + w\) 且 \(t=f\)。\(T_{f}\) 是简写（例如，\(w = 2\) 的 T4）。
分级压缩和分层压缩在中心表现相同：\(w = 0\) 且 \(f = t = 2\)。简写为 \(w = 0\) 的 N。

分级压缩以牺牲写入为代价来改进读取，并且随着 \(f\) 的增加而接近排序数组，而分层压缩以牺牲读取为代价来优先考虑写入，并且随着 \(f\) 的增加而接近无序日志。

UCS 允许为每个级别单独定义 \(w\) 的值；因此，级别可以具有不同的行为。例如，级别零可以使用分层压缩（类似于 STCS），而更高级别可以使用分级压缩（类似于 LCS），定义为具有越来越高的读取优化级别。

基于大小的分级

该策略在特定分片边界处拆分 SSTable，这些边界数量随着 SSTable 密度的增加而增加。拆分创建的 SSTable 之间的非重叠使并发压缩成为可能。但是，让我们暂时忽略密度和拆分，并探索如果 SSTable 从未拆分，它们是如何分组到级别的。

Memtable 被刷新到级别零 (L0)，并且 memtable 刷新大小 \(s_{f}\) 计算为刷新 memtable 时写入的所有 SSTable 的平均大小。此参数 \(s_{f}\) 旨在形成层次结构的基础，所有新刷新的 SSTable 最终都将位于其中。使用固定的扇出因子 \(f\) 和 \(s_{f}\)，大小为 \(s\) 的 SSTable 的级别 \(L\) 计算如下

\[L = \begin{cases} \left \lfloor \log_f {\frac{s}{s_{f}}} \right \rfloor & \text{if } s \ge s_{f} \\ 0 & \text{otherwise} \end{cases}\]

SSTable 根据其大小分配到级别

级别	最小 SSTable 大小	最大 SSTable 大小
0	0	\(s_{f} \cdot f\)
1	\(s_{f} \cdot f\)	\(s_{f} \cdot f^2\)
2	\(s_{f} \cdot f^2\)	\(s_{f} \cdot f^3\)
3	\(s_{f} \cdot f^3\)	\(s_{f} \cdot f^4\)
…	…	…
n	\(s_{f} \cdot f^n\)	\(s_{f} \cdot f^{n+1}\)

级别

最小 SSTable 大小

最大 SSTable 大小

\(s_{f} \cdot f\)

\(s_{f} \cdot f^2\)

\(s_{f} \cdot f^3\)

\(s_{f} \cdot f^4\)

…

\(s_{f} \cdot f^n\)

\(s_{f} \cdot f^{n+1}\)

一旦 SSTable 开始在级别中累积，当一个级别中的 SSTable 数量超过前面讨论的阈值 \(t\) 时，就会触发压缩

\(t = 2\)，分级压缩
1. 大小为 \(\ge s_{f} \cdot f^n\) 的 SSTable 被提升到级别 \(n\)。
2. 当第二个 SSTable 被提升到该级别（大小也为 \(\ge s_{f} \cdot f^n\)）时，它们会压缩并形成一个大小为 \(\sim 2s_{f} \cdot f^n\) 的新 SSTable，位于相同级别，前提是 \(f > 2\)。
3. 在至少重复 \(f-2\) 次之后（即，总共 \(f\) 个 SSTable 进入该级别），压缩结果增长到 \(\ge s_{f} \cdot f^{n+1}\) 并进入下一级。
\(t = f\)，分层压缩
- 在 \(f\) 个 SSTable 进入级别 \(n\) 之后，每个 SSTable 的大小都为 \(\ge s{f} \cdot f^n\)，它们会压缩并形成一个大小为 \(\ge s_{f} \cdot f^{n+1}\) 的新 SSTable，位于下一级。

在这些方案中，覆盖和删除被忽略，但如果已知覆盖/删除的预期比例，则可以调整算法。当前的 UCS 实现执行此调整，但目前不公开调整。

RA 和 WA 的估计

每种压缩策略的读写放大与层次结构中的级别数量成正比

策略	写入放大	读取放大
分级	\(\varpropto\) 级别数量的 \(f-1\) 倍	\(\varpropto\) 级别数量
分层	\(\varpropto\) 级别数量	\(\varpropto\) 级别数量的 \(f-1\) 倍

策略

写入放大

读取放大

分级

\(\varpropto\) 级别数量的 \(f-1\) 倍

\(\varpropto\) 级别数量

分层

\(\varpropto\) 级别数量

\(\varpropto\) 级别数量的 \(f-1\) 倍

级别数量

使用最大数据集大小 \(D\)，级别数量可以计算如下

\[L = \begin{cases} \left \lfloor \log_f {\frac {D}{s_{f}}} \right \rfloor & \text{if } D \ge s_{f} \\ 0 & \text{otherwise} \end{cases}\]

此计算基于以下假设：当所有级别都已满时，最大数据集大小 \(D\) 会达到，并且最大级别数量与 \(f\) 的对数成反比。

因此，当我们尝试控制数据库压缩的开销时，我们有一个策略选择空间，范围从

分层压缩（\(t=2\)）具有高\(f\)
- 较少的层级数
- 高读取效率
- 高写入成本
- 随着\(f\)的增加，更接近于排序数组的行为
压缩，其中\(t = f = 2\)，分层与分级相同，我们有一个中间地带，具有对数增加的读写成本；
分级压缩（\(t=f\)）具有高\(f\)
- 非常多的SSTables
- 低读取效率
- 低写入成本
- 随着\(f\)的增加，更接近于无序日志

这可以通过用所有较低层级的扇出因子的乘积替换指数运算，轻松推广到不同的扇出因子

级别	最小 SSTable 大小	最大 SSTable 大小
0	0	\(s_{f} \cdot f_0\)
1	\(s_{f} \cdot f_0\)	\(s_{f} \cdot f_0 \cdot f_1\)
2	\(s_{f} \cdot f_0 \cdot f_1\)	\(s_{f} \cdot f_0 \cdot f_1 \cdot f_2\)
…	…	…
n	\(s_{f} \cdot \prod_{i < n} f_i\)	\(s_{f} \cdot \prod_{i\le n} f_i\)

级别

最小 SSTable 大小

最大 SSTable 大小

\(s_{f} \cdot f_0\)

\(s_{f} \cdot f_0 \cdot f_1\)

\(s_{f} \cdot f_0 \cdot f_1 \cdot f_2\)

…

\(s_{f} \cdot \prod_{i < n} f_i\)

\(s_{f} \cdot \prod_{i\le n} f_i\)

基于密度的分层

如果我们将之前讨论中的大小\(s\)替换为密度度量

\[d = \frac s v\]

其中\(v\)是SSTable覆盖的令牌空间的比例，所有公式和结论仍然有效。但是，使用密度，输出现在可以分割在任意点。如果多个SSTables被压缩和分割，形成的新SSTables将比原始SSTables更密集。例如，使用T4的缩放参数，四个输入SSTables，每个SSTables跨越令牌空间的1/10，当压缩和分割时，将形成四个新的SSTables，每个SSTables跨越令牌空间的1/40。

这些新的SSTables将具有相同的大小，但密度更高，因此将移动到下一级，因为更高的密度值超过了原始压缩级别的最大密度。如果我们能确保分割点是固定的（见下文），这个过程将对每个分片（令牌范围）重复，并行执行独立的压缩。

在计算\(v\)时，必须考虑本地拥有的令牌份额。因为虚拟节点意味着节点的本地令牌所有权不是连续的，所以第一个和最后一个令牌之间的差异不足以计算令牌份额；因此，必须排除任何非本地拥有的范围。

使用密度度量，我们可以通过分片来控制SSTables的大小，以及并行执行压缩。使用大小分层压缩，我们可以通过将数据预先分割成固定数量的压缩分片来实现并行化，这些分片基于数据目录。但是，该方法要求分片的数量预先确定，并且在层次结构的所有级别上都相等，并且SSTables可能变得太小或太大。大型SSTables会使流式传输和修复变得复杂，并增加压缩操作的持续时间，将资源固定在长时间运行的操作中，并使更多SSTables在层次结构的较低级别上累积的可能性更大。

基于密度分层压缩允许更广泛的分割选项。例如，SSTables的大小可以保持接近选定的目标，允许UCS处理STCS（SSTable大小随每个级别增长）和LCS（令牌份额随每个级别缩小）的级别。

分片

基本分片方案

这种分片机制独立于压缩规范。对于分割SSTables，有一系列选择

当达到某个输出大小时分割（如LCS），形成非重叠的SSTable运行，而不是单个SSTables
将令牌空间分割成预定义边界点的分片
在预定义边界处分割，但前提是达到某个最小大小

仅按大小分割会导致单个SSTables具有不同的起始位置。要压缩以这种方式分割的SSTables，您必须选择按顺序压缩一个级别的整个令牌范围，或者由于SSTables重叠，而必须多次压缩和复制一些数据。如果使用预定义边界点，一些令牌范围可能更稀疏，输入更少，并且会使结果SSTables的密度倾斜。如果发生这种情况，可能需要进一步分割。在混合选项中，密度倾斜发生的频率较低，但仍然可能发生。

为了避免这些问题并允许并行压缩压缩层次结构的所有级别，UCS为每次压缩预定义边界点，并且始终在这些点分割SSTables。边界数量由输入SSTables的密度和结果SSTables的估计密度决定。随着密度的增大，边界数量增加，使单个SSTables的大小保持接近预定义的目标。使用指定基本计数的2的幂倍数，即在中间分割分片，确保适用于给定输出密度的任何边界也适用于所有更高的密度。

可以配置两个分片参数

基本分片计数\(b\)
目标SSTable大小\(s_{t}\)

在每次压缩开始时，请记住，输出的密度\(d\)是根据SSTables的输入大小\(s\)和令牌范围\(v\)估计的

\[d = \frac s v\]

其中\(v\)是输入SSTables覆盖的令牌范围的比例，值为0到1。\(v = 1\)表示整个令牌范围都被输入SSTables覆盖，\(v = 0\)表示输入SSTables没有覆盖任何令牌范围。

当将memtable首次刷新到L0时，\(v = 1\)，因为整个令牌范围都包含在memtable中。在随后的压缩中，令牌范围\(v\)是被压缩的SSTables覆盖的令牌范围的比例。

使用计算出的输出密度，加上\(b\)和\(s_{t}\)的值，可以计算出将令牌空间分割成的分片数量\(S\)

\[S = \begin{cases} b & \text{if } {\frac d s_{t} \cdot \frac 1 b} < 1 \\ 2^{\left\lfloor \log_2 \left( {\frac d s_{t} \cdot \frac 1 b}\right)\right\rceil} \cdot b & \text{if } {\frac d s_{t} \cdot \frac 1 b} \ge 1 \\ \end{cases}\]

其中\(\lfloor x \rceil\)表示\(x\)四舍五入到最接近的整数，即\(\lfloor x + 0.5 \rfloor\)。因此，在第二种情况下，密度除以目标大小并四舍五入到\(b\)的2的幂倍数。如果结果小于1，分片数量将是基本分片计数，因为memtable被分割成\({2 \cdot b}\)，或\(b\)个L0分片。

但是，令牌范围并不是唯一影响我们是否在\(b\)个分片之间切换（条件大于或等于1）的因素。如果memtable非常大，并且能够一次刷新多个千兆字节，\(d\)可能比\(s_{t}\)大一个数量级，并导致SSTables即使在L0上也分割成多个分片。相反，如果memtable很小，\(d\)在L0以上级别上可能仍然小于\(s_{t}\)，其中条件小于1，因此将有stem[b]个分片。

\(S - 1\)个边界被生成，将本地令牌空间平均分割成\(S\)个分片。分割本地令牌空间将分割这些边界上的压缩结果，为每个分片形成一个单独的SSTable。生成的SSTables的大小将在\(s_{t}/\sqrt 2\)和\(s_{t} \cdot \sqrt 2\)之间。

例如，让我们使用\(s_{t} = 100MiB\)的目标SSTable大小和\(b = 4\)个基本分片。如果\(s_{f} = 200 MiB\)的输入memtable被刷新，计算分片数量的条件是

\[\frac{200}{100} \cdot \frac{1}{4} = 0.5 < 1\]

此计算结果为\(0.5 < 1\)，因为初始刷新的\(v\)值为1。因为结果小于1，所以使用基本分片计数，memtable被分割成四个大约50MiB的L0分片。每个分片跨越令牌空间的1/4。

为了继续这个例子，在下一级压缩中，对于四个分片中的一个，让我们压缩六个50 MiB的SSTables。输出的估计密度将是

\[\left( \frac{6 \cdot 50\, \mathrm{MiB}}{\frac{1}{4}} \right) = 1200 \mathrm{MiB}\]

使用1/4作为输入SSTables覆盖的令牌范围的\(v\)值。

分割的条件将是

\[(\frac{1200}{100} \cdot \frac{1}{4}) = 3 > 1\]

因此，分片数量将计算为

\[2^{\left\lfloor \log_2 \left( {\frac{1200}{100} \cdot \frac{1}{4}}\right)\right\rceil} \cdot b\]

或\(2^{\log_2 3}\)，四舍五入到\(2^2 \cdot 4\)个分片，用于整个本地令牌空间，以及覆盖令牌空间的1/4的压缩。假设没有覆盖或删除，生成的SSTables的大小将为75 MiB，令牌份额为1/16，密度为1200 MiB。

完整分片方案

这种分片方案可以轻松扩展。目前实现了两个扩展，SSTable增长和最小SSTable大小。

首先，让我们检查一下当数据集的大小预计会变得非常大时的情况。为了避免预先指定足够大的目标大小以避免每个SSTable开销带来的问题，已经实现了SSTtable增长参数。此参数决定了密度增长的哪一部分应该分配给SSTable大小的增加，从而减少分片数量的增长，因此减少非重叠的SSTables。

第二个扩展是具有固定分片数量的操作模式，该模式在达到最小大小后有条件地分割。定义最小SSTable大小，每当分割会导致SSTables小于提供的最小值时，基本分片计数就会减少。

有四个用户定义的分片参数

基本分片计数\(b\)
目标SSTable大小\(s_{t}\)
最小SSTable大小\(s_{m}\)
SSTable增长组件\(\lambda\)

给定密度\(d\)的分片数量\(S\)计算为

\[S = \begin{cases} 1 & \text{if } d < s_{m} \\ \min(2^{\left\lfloor \log_2 \frac {d}{s_{m}} \right\rfloor}, x) & \text{if } d < s_{m} \cdot b \text{, where } x \text{ is the largest power of 2 divisor of } b \\ b & \text{if } d < s_{t} \cdot b \\ 2^{\left\lfloor (1-\lambda) \cdot \log_2 \left( {\frac {d}{s_{t}} \cdot \frac 1 b}\right)\right\rceil} \cdot b & \text{otherwise} \end{cases}\]

这些参数的一些有用组合

上面的基本方案使用 SSTable 增长率 \(\lambda=0\) 和最小 SSTable 大小 \(s_{m}=0\)。下面的图表展示了基准分片数量 \(b=4\) 和目标 SSTable 大小 \(s_{t} = 1\, \mathrm{GB}\) 的行为。

Graph with lambda 0

使用 \(\lambda = 0.5\) 会使分片数量和 SSTable 大小均匀增长。当密度增加四倍时，分片数量和该密度带的预期 SSTable 大小都会翻倍。下面的示例使用 \(b=8\), \(s_{t} = 1\, \mathrm{GB}\) 并且还应用了最小大小 \(m = 100\, \mathrm{MB}\)。

Graph with lambda 0.5

类似地，\(\lambda = 1/3\) 使 SSTable 增长成为密度增长的三次方根，即 SSTable 大小随着分片数量增长的平方根而增长。下面的图表使用 \(b=1\) 和 \(s_{t} = 1\, \mathrm{GB}\)（注意：当 \(b=1\) 时，最小大小没有影响）。

Graph with lambda 0.33

增长系数为 1 会构建一个在每一层都有 \(b\) 个分片的层次结构。与最小 SSTable 大小相结合，操作模式使用预先指定的分片数量，但只有在达到最小大小后才会进行拆分。下面以 \(b=10\) 和 \(s_{m} = 100\, \mathrm{MB}\) 为例（注意：当 \(\lambda=1\) 时，目标 SSTable 大小无关紧要）。

Graph with lambda 1

选择要压缩的 SSTable

密度均衡将 SSTable 分隔成由压缩配置的扇出因子定义的层级。但是，与大小均衡不同，大小均衡中预计 SSTable 会覆盖整个令牌空间，而层级上的 SSTable 数量不能用作触发器，因为可能存在不重叠的 SSTable。在这种情况下，读取查询效率较低。为了解决这个问题，执行分片，在层级上同时执行多个压缩，并减小单个压缩操作的大小。不重叠的部分必须分成不同的桶，桶中重叠的 SSTable 数量决定了要执行的操作。桶是将一起压缩的选定 SSTable 集。

首先形成一个满足以下要求的最小重叠集列表。

两个不重叠的 SSTable 永远不会放在同一个集中。
如果两个 SSTable 重叠，则列表中有一个集包含这两个 SSTable。
SSTable 在列表中按顺序排列。

第二个条件也可以重新表述为：对于令牌范围中的任何点，列表中都存在一个集，该集包含所有范围覆盖该点的 SSTable。换句话说，重叠集为我们提供了读取任何键时需要查询的最大 SSTable 数量，即我们的触发器 \(t\) 旨在控制的读取放大。我们不会计算或存储重叠集覆盖的确切范围，只存储参与的 SSTable。这些集可以在 \(O(n\log n)\) 时间内获得。

例如，如果 SSTable A、B、C 和 D 分别覆盖令牌 0-3、2-7、6-9 和 1-8，我们计算一个重叠集列表，即 ABD 和 BCD。 A 和 C 不重叠，因此它们必须在不同的集中。 A、B 和 D 在令牌 2 处重叠，因此必须至少存在一个集，类似地，B、C 和 D 在 7 处重叠。只有 A 和 D 在 1 处重叠，但集 ABD 已经包含了这种组合。

这些重叠集足以决定是否应该执行压缩，当且仅当一个集中元素的数量至少与 \(s_{t}\) 一样大。但是，我们可能需要在压缩中包含比这个集本身更多的 SSTable。

我们的分片方案可能会最终构建跨越同一层级的不同大小分片的 SSTable。一个明显的例子是层级压缩的情况。在这种情况下，SSTable 在某个密度处进入，在第一次压缩后，生成的 SSTable 比初始密度大 2 倍，导致 SSTable 在令牌范围的中间分成两半。当另一个 SSTable 进入同一层级时，我们将有两个较旧的 SSTable 和新 SSTable 之间的单独重叠集。为了提高效率，接下来触发的压缩需要选择这两个重叠集。

为了处理部分重叠的情况，重叠集将与所有共享一些 SSTable 的相邻重叠集进行传递扩展。因此，构建的所有 SSTable 集都具有一些重叠 SSTable 链，将它们连接到初始集。这个扩展集形成了压缩桶。

除了 TRANSITIVE 之外，还实现了 NONE 和 SINGLE 的“重叠包含方法”以进行实验，但它们不推荐用于 UCS 分片方案。

在正常操作中，我们压缩压缩桶中的所有 SSTable。如果压缩非常晚，我们可能会对压缩的重叠源数量施加限制。在这种情况下，我们使用最旧的 SSTable 集合，这些 SSTable 在任何包含的重叠集中最多选择 limit-many 个，确保如果一个 SSTable 包含在这个压缩中，所有较旧的 SSTable 也包含在内以保持时间顺序。

选择要运行的压缩

压缩策略旨在最大程度地减少查询的读取放大，读取放大由任何给定键上重叠的 SSTable 数量定义。为了在压缩延迟的情况下获得最高效率，选择具有最高重叠的压缩桶作为所有可能的选择。如果有多个选择，则在每个层级内均匀随机选择一个。在层级之间，优先选择最低层级，因为对于相同的工作量，预计它会覆盖令牌空间的更大比例。

在持续负载下，这种机制可以防止 SSTable 在某些层级上累积，而这在传统策略中有时会发生。使用较旧的策略，所有资源都可能被 L0 和在 L1 上累积的 SSTable 消耗。使用 UCS，可以实现一个稳态，其中压缩始终使用比分配的阈值和扇出因子更多的 SSTable，并根据它们能够为负载维持的最低重叠来维护分层层次结构。

主要压缩

在 UCS 的工作原理下，主要压缩是一个操作，它将所有具有（传递）重叠的 SSTable 压缩在一起，并将输出拆分成适合预期结果密度的分片边界。

换句话说，主要压缩将导致 \(b\) 个并发压缩，每个压缩都包含每个基本分片中覆盖的所有 SSTable。结果将在分片边界上拆分，分片边界数量取决于分片中包含的数据的总大小。

与 STCS 和 LCS 的区别

请注意，分层 UCS 与传统 STCS 之间，以及层级 UCS 与传统 LCS 之间存在一些差异。

分层 UCS 与 STCS

STCS 与 UCS 非常相似。但是，STCS 通过查找大小相似的 SSTable 来定义桶/层级，而不是使用预定义的大小分组。因此，STCS 最终可能会选择一些奇怪的桶，跨越大小差异很大的 SSTable；UCS 的选择更稳定和可预测。

STCS 在某个桶上找到至少 min_threshold 个 SSTable 时会触发压缩，并且它会一次从该桶中压缩 min_threshold 到 max_threshold 个 SSTable。 min_threshold 等效于 UCS 的 \(t = f = w + 2\)。 UCS 放弃了上限，因为它的压缩在非常多的 SSTable 情况下仍然很有效。

UCS 使用密度度量来拆分结果，以保持 SSTable 的大小和压缩时间较低。在一个层级内，UCS 只会在决定是否达到阈值时考虑重叠的 SSTable，并且会独立地压缩不重叠的 SSTable 集。

如果在一个桶内有多个选择来选择 SSTable，STCS 会按大小对它们进行分组，而 UCS 会按时间戳对它们进行分组。因此，STCS 很容易丢失时间顺序，这使得整个表过期效率降低。 UCS 有效地跟踪时间顺序和整个表过期。由于 UCS 可以应用整个表过期，因此此功能对于具有生存时间约束的时间序列数据也很有用。

UCS-层级与 LCS

与 UCS 相比，LCS 的行为似乎大不相同。但是，这两种策略实际上非常相似。

LCS 使用每个层级上的多个 SSTable 来形成一个排序的非重叠 SSTable 运行，这些 SSTable 的大小固定且较小。因此，随着层级增加，物理 SSTable 的数量（按 fanout_size 因子）而不是大小增加。通过这种方式，LCS 减少了空间放大并确保了更短的压缩时间。当层级上运行的组合大小超过预期时，它会选择一些 SSTable 与来自层次结构下一层级的重叠 SSTable 进行压缩。最终，下一层级的大小会超过其大小限制，并触发更高层级的操作。

在 UCS 中，随着层级增加，SSTable 的密度按扇出因子 \(f\) 增加。当在分片层级上找到第二个重叠的 SSTable 时，会触发压缩。 UCS 会压缩该层级上的重叠桶，结果通常也会出现在该层级上。但最终，数据会达到下一层级的足够大小。在数据均匀分布的情况下，UCS 和 LCS 的行为类似，压缩在相同的时间范围内触发。

这两种方法最终会产生非常相似的效果。 UCS 具有额外的优势，即压缩不会影响其他层级。在 LCS 中，L0 到 L1 的压缩可能会阻止任何并发 L1 到 L2 的压缩，这是一种不幸的情况。在 UCS 中，SSTable 的结构使得它们可以轻松地切换到分层 UCS 或使用不同的参数设置进行更改。

由于 LCS SSTable 仅基于大小，因此在拆分位置上有所不同，当 LCS 选择 SSTable 在下一层级上进行压缩时，会包含一些仅部分重叠的 SSTable。因此，SSTable 可能比严格必要时更频繁地进行压缩。

UCS 通过在特定令牌边界上进行分片来处理空间放大问题。 LCS 根据固定大小拆分 SSTable，边界通常落在下一层级上的 SSTable 内部，比必要时更频繁地启动压缩。因此，UCS 有助于严格控制写入放大。这些边界保证我们可以有效地选择与低密度 SSTable 的跨度完全匹配的高密度 SSTable。

UCS 选项

子属性描述

子属性	描述
enabled	启用后台压缩。默认值：true
only_purge_repaired_tombstone	启用此属性可以防止数据在 `gc_grace_seconds` 内未运行修复时恢复。默认值：false
scaling_parameters	每个层级的缩放参数列表，指定为 \(L_{f}\)、\(T_{f}\)、\(N\)，或一个整数，直接指定 \(w\)。如果存在比此列表长度更多的层级，则最后一个值将用于所有更高层级。通常这将是一个参数，指定层次结构所有层级的行为。层级压缩，指定为 \(L_{f}\)，更适合读取密集型工作负载，尤其是当布隆过滤器无效时（例如，使用宽分区）；更高的层级扇出因子会提高读取放大（因此会提高延迟，以及读取为主的工作负载的吞吐量），但会增加写入成本。等效于传统 LCS 的是 L10。分层压缩，指定为 \(T_{f}\)，更适合写入密集型工作负载，或可以利用布隆过滤器或时间顺序的工作负载；更高的分层扇出因子会提高写入成本（因此会提高吞吐量），但会使读取变得更加困难。 \(N\) 是介于两者之间的选择，它具有层级（每个层级一个 SSTable 运行）和分层（一个压缩被提升到下一层级）以及扇出因子为 2 的特性。此值也可以指定为 T2 或 L2。默认值：T4（阈值为 4 的 STCS）
target_sstable_size	目标 SSTable 大小 \(s_{t}\)，以人类友好的字节大小指定，例如 MiB。该策略将把数据分成多个分片，目标是生成大小介于 \(s_{t}/\sqrt{2}\) 和 \(s_{t} \cdot \sqrt{2}\) 之间的 SSTable。较小的 SSTable 提高了流式传输和修复效率，并缩短了压缩时间。另一方面，磁盘上的每个 SSTable 都有一个非平凡的内存占用，也会影响垃圾回收时间。如果系统中 SSTable 数量带来的内存压力过高，请增加此值。默认值：1 GiB
min_sstable_size	最小 SSTable 大小，适用于当基本分片数量会导致被认为太小的 SSTable 时。如果设置了此值，该策略将把空间分成少于基本数量的分片，以使估计的 SSTable 大小至少与该值一样大。值为 0 将禁用此功能。默认值：100MiB
base_shard_count	最小分片数量 \(b\)，用于密度最小的级别。这为最低级别提供了最小的压缩并发性。较小的数字会导致更大的 L0 SSTable，但可能会限制整体最大写入吞吐量（因为每条数据都必须经过 L0）。默认值：4（系统表为 1，或当定义了多个数据位置时）
sstable_growth	SSTable 增长组件 \(\lambda\)，作为分片指数计算中的一个因子应用。这是一个介于 0 和 1 之间的数字，它控制着密度增长应用于单个 SSTable 大小的部分和增加分片数量的部分。使用值为 1 的效果是将分片数量固定为基本值。使用 0.5 使分片数量和 SSTable 大小随着密度增长的平方根而增长。这对于减少为非常大的数据集创建的 SSTable 的数量很有用。例如，如果没有增长校正，一个 10TiB 的数据集，目标大小为 1GiB，将导致超过 10K 个 SSTable。如此多的 SSTable 会导致过高的开销，包括每个 SSTable 结构使用的堆内内存，以及在压缩期间查找交叉 SSTable 和跟踪重叠集的查找时间。例如，对于基本分片数量为 4，增长因子可以将潜在的 SSTable 数量减少到约 160 个，大小约为 64GiB，在内存开销、单个压缩持续时间和空间开销方面都是可控的。可以调整参数，增加该值以在顶层获得更少但更大的 SSTable，并减少该值以支持更多数量的更小的 SSTable。默认值：0.333（SSTable 大小随着分片数量增长的平方根而增长）
expired_sstable_check_frequency_seconds	确定检查过期 SSTable 的频率。默认值：10 分钟
max_sstables_to_compact	一次操作中要压缩的 SSTable 的最大数量。较大的值可能会减少写入放大，但会导致非常长的压缩，从而在进行此类压缩时导致非常高的读取放大开销。默认值旨在控制操作的长度，并在压缩进行时防止 SSTable 累积。如果扇出因子大于 SSTable 的最大数量，该策略将忽略后者。默认值：无（尽管 32 是一个不错的选择）
overlap_inclusion_method	指定如何将重叠部分扩展到桶中。TRANSITIVE 确保如果我们选择一个 SSTable 进行压缩，我们也会压缩与它重叠的 SSTable。SINGLE 只执行一次此扩展（即它只选择与原始重叠 SSTable 部分重叠的 SSTable。NONE 不添加任何重叠的 SSTable。不推荐使用 NONE，SINGLE 可能会以重新压缩一些数据为代价提供更多并行性，这些数据是在从 LCS 升级或在范围移动期间重新压缩的。默认值：TRANSITIVE
unsafe_aggressive_sstable_expiration	过期 SSTable 会被删除，而不会检查它们的数据是否正在遮蔽其他 SSTable。只有在 `cassandra.allow_unsafe_aggressive_sstable_expiration` 为真时才能启用此标志。打开此标志可能会导致正确性问题，例如已删除数据的重新出现。有关有效用例和潜在问题的讨论，请参阅 CASSANDRA-13418。默认值：false

enabled

启用后台压缩。

默认值：true

only_purge_repaired_tombstone

启用此属性可以防止数据在 gc_grace_seconds 内未运行修复时恢复。

默认值：false

scaling_parameters

每个层级的缩放参数列表，指定为 \(L_{f}\)、\(T_{f}\)、\(N\)，或一个整数，直接指定 \(w\)。如果存在比此列表长度更多的层级，则最后一个值将用于所有更高层级。通常这将是一个参数，指定层次结构所有层级的行为。

层级压缩，指定为 \(L_{f}\)，更适合读取密集型工作负载，尤其是当布隆过滤器无效时（例如，使用宽分区）；更高的层级扇出因子会提高读取放大（因此会提高延迟，以及读取为主的工作负载的吞吐量），但会增加写入成本。等效于传统 LCS 的是 L10。

分层压缩，指定为 \(T_{f}\)，更适合写入密集型工作负载，或可以利用布隆过滤器或时间顺序的工作负载；更高的分层扇出因子会提高写入成本（因此会提高吞吐量），但会使读取变得更加困难。

\(N\) 是介于两者之间的选择，它具有层级（每个层级一个 SSTable 运行）和分层（一个压缩被提升到下一层级）以及扇出因子为 2 的特性。此值也可以指定为 T2 或 L2。

默认值：T4（阈值为 4 的 STCS）

target_sstable_size

目标 SSTable 大小 \(s_{t}\)，以人类友好的字节大小指定，例如 MiB。该策略将把数据分成多个分片，目标是生成大小介于 \(s_{t}/\sqrt{2}\) 和 \(s_{t} \cdot \sqrt{2}\) 之间的 SSTable。较小的 SSTable 提高了流式传输和修复效率，并缩短了压缩时间。另一方面，磁盘上的每个 SSTable 都有一个非平凡的内存占用，也会影响垃圾回收时间。如果系统中 SSTable 数量带来的内存压力过高，请增加此值。

默认值：1 GiB

min_sstable_size

最小 SSTable 大小，适用于当基本分片数量会导致被认为太小的 SSTable 时。如果设置了此值，该策略将把空间分成少于基本数量的分片，以使估计的 SSTable 大小至少与该值一样大。值为 0 将禁用此功能。

默认值：100MiB

base_shard_count

最小分片数量 \(b\)，用于密度最小的级别。这为最低级别提供了最小的压缩并发性。较小的数字会导致更大的 L0 SSTable，但可能会限制整体最大写入吞吐量（因为每条数据都必须经过 L0）。

默认值：4（系统表为 1，或当定义了多个数据位置时）

sstable_growth

SSTable 增长组件 \(\lambda\)，作为分片指数计算中的一个因子应用。这是一个介于 0 和 1 之间的数字，它控制着密度增长应用于单个 SSTable 大小的部分和增加分片数量的部分。使用值为 1 的效果是将分片数量固定为基本值。使用 0.5 使分片数量和 SSTable 大小随着密度增长的平方根而增长。这对于减少为非常大的数据集创建的 SSTable 的数量很有用。例如，如果没有增长校正，一个 10TiB 的数据集，目标大小为 1GiB，将导致超过 10K 个 SSTable。如此多的 SSTable 会导致过高的开销，包括每个 SSTable 结构使用的堆内内存，以及在压缩期间查找交叉 SSTable 和跟踪重叠集的查找时间。例如，对于基本分片数量为 4，增长因子可以将潜在的 SSTable 数量减少到约 160 个，大小约为 64GiB，在内存开销、单个压缩持续时间和空间开销方面都是可控的。可以调整参数，增加该值以在顶层获得更少但更大的 SSTable，并减少该值以支持更多数量的更小的 SSTable。

默认值：0.333（SSTable 大小随着分片数量增长的平方根而增长）

expired_sstable_check_frequency_seconds

确定检查过期 SSTable 的频率。

默认值：10 分钟

max_sstables_to_compact

一次操作中要压缩的 SSTable 的最大数量。较大的值可能会减少写入放大，但会导致非常长的压缩，从而在进行此类压缩时导致非常高的读取放大开销。默认值旨在控制操作的长度，并在压缩进行时防止 SSTable 累积。如果扇出因子大于 SSTable 的最大数量，该策略将忽略后者。

默认值：无（尽管 32 是一个不错的选择）

overlap_inclusion_method

指定如何将重叠部分扩展到桶中。TRANSITIVE 确保如果我们选择一个 SSTable 进行压缩，我们也会压缩与它重叠的 SSTable。SINGLE 只执行一次此扩展（即它只选择与原始重叠 SSTable 部分重叠的 SSTable。NONE 不添加任何重叠的 SSTable。不推荐使用 NONE，SINGLE 可能会以重新压缩一些数据为代价提供更多并行性，这些数据是在从 LCS 升级或在范围移动期间重新压缩的。

默认值：TRANSITIVE

unsafe_aggressive_sstable_expiration

过期 SSTable 会被删除，而不会检查它们的数据是否正在遮蔽其他 SSTable。只有在 cassandra.allow_unsafe_aggressive_sstable_expiration 为真时才能启用此标志。打开此标志可能会导致正确性问题，例如已删除数据的重新出现。有关有效用例和潜在问题的讨论，请参阅 CASSANDRA-13418。